Logical Data Modeling - Reflexive relationship property
About
reflexive is a relationship property that indicates:
- that the relationship relates every element to itself.
- in other word, that the relation set representing the relationship contains every tuple:
- in a binary relationship - the relation set contains all <a,b> such as a=b
- in a N relationship: <a,b,c..., n> such as a=b=c…=n
Mathematical Definition
A binary relation Rel is called reflexive:
- on a a dimensional set A, if the relation set contains every tuple <a, b> for every element a of A.
<MATH> \{(a)\in\Bbb A\mid a = a\} \in Rel </MATH>
Example
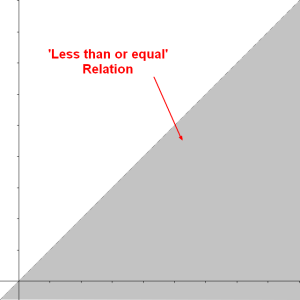
Less than or equal
The relation less than or equal to (<=) on the set of integers {1, 2, 3} is the following set of tuple
<1, 1>,
<1, 2>,
<1, 3>,
<2, 2>,
<2, 3>,
<3, 3>
It is reflexive because the tuples <1, 1>, <2, 2>, <3, 3> are in this relation.
As a matter of fact, this relation is reflexive on any set of numbers (not only integer but also real numbers, …).
Against the <math>R</math> , the relation less than or equal to is the below gray area in <math>R^2</math>
Equivalence relationship
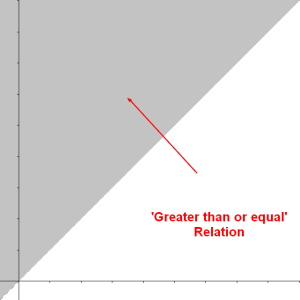
Similarly and because every number is equal to itself, the relation greater than or equal and is equal to on any set of numbers are reflexive.
Plot
A few relations:
- between x and y
- on subsets of <math>R</math> (real number)
- represented as subsets of <math>R^2</math>
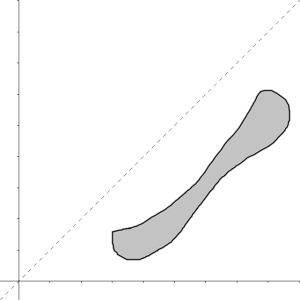
The gray area is the relation.
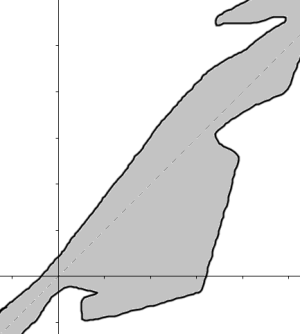
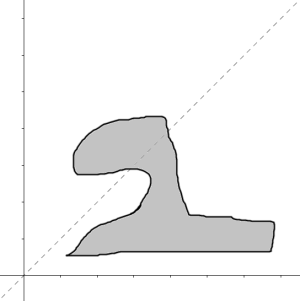
In the set of real number, a relation is reflexive if it contains the dotted line y=x
Example:
- Because the line y=x is in the relation, this is then a reflexive relation (but it's not symmetric, nor antisymmetric)
- Because the line y=x is in the relation, this is a reflexive relation (and it's symmetric)
- Because the line y=x is partially in relation, this is NOT a reflexive relation (nor symmetric or antisymmetric )
- Because the line y=x is not in the relation, this is then NOT a reflexive relation (but it's an antisymmetric)