linear_algebra:graph

About

Articles Related

Minimum Spanning Forest

Graph Analysis - Minimum spanning forest

Formulation

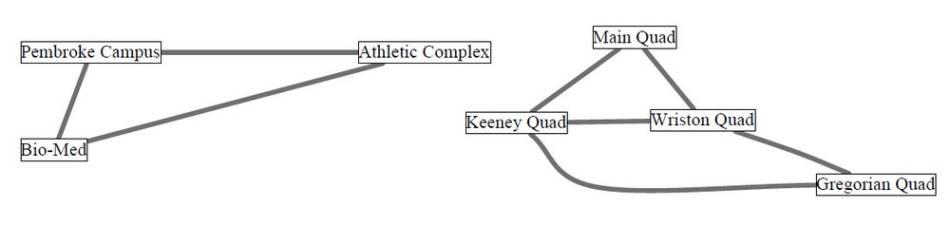
Formulating GF(2) vector: subset {Pembroke, Main, Gregorian} is represented by:

Pembroke	Athletic	Bio-Med	Main	Keeney	Wriston	Gregorian
1			1			1

Edge Representation in term of vectors:

Edge	Vector
	Pembroke	Athletic	Bio-Med	Main	Keeney	Wriston	Gregorian
{Pembroke, Athletic}	1	1
{Pembroke, Bio-Med}	1		1
{Athletic, Bio-Med}		1	1
{Main, Keeney}				1	1
{Main, Wriston}				1		1
{Keeney, Wriston}					1	1
{Keeney, Gregorian}					1		1
{Wriston, Gregorian}						1	1

The vector representing {Keeney, Gregorian} is the sum, for example, of the vectors representing {Keeney, Main }, {Main, Wriston}, and {Wriston, Gregorian}.

A vector with 1’s in entries x and y is the sum of vectors corresponding to edges that form an x-to-y path in the graph. For instance, the span of the vectors representing {Pembroke, Bio-Med}, {Main, Wriston}, {Keeney, Wriston}, {Wriston, Gregorian }

contains the vectors corresponding to

{Main, Keeney}, {Keeney, Gregorian}, and {Main, Gregorian}

but not the vectors corresponding to

{Athletic, Bio-Med } or {Bio-Med, Main}

Algorithm

def Grow(G)
    S := 0; 
    consider the edges in increasing order
    for each edge e:
        if e’s endpoints are not yet connected
             add e to S.

def Grow(V)
    S = 0; 
    repeat while possible:
        find a vector v in V not in Span S,
        and put it in S.

Considering edges e of G corresponds to considering vectors v in V
Testing if e’s endpoints are not connected corresponds to testing if v is not in Span S.

The Grow algorithm for MSF is a specialization of the Grow algorithm for vectors. Same for the Shrink algorithms.

Basis

One kind of basis in a graph G: a set S of edges forming a spanning forest.

Spanning: for each edge xy in G, there is an x-to-y path consisting of edges of S.
Independent: no cycle consisting of edges of S

A basis for a graph is a spanning forest. Unique Representation shows that, for each edge xy in the graph,

there is an x-to-y path in the spanning forest, and
there is only one such path.

Table of Contents