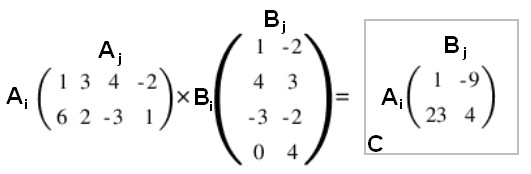Linear Algebra - Matrix Matrix (Multiplication)
About
Matrix Matrix (Multiplication) definition .
Two matrices may be multiplied when they are conformable: ie the number of columns in the first matrix is equal to the number of rows in the second matrix.
If they are of the same Linear Algebra - Matrix, just transpose one
Articles Related
Definition
Three ways to multiply a matrix with a matrix:
- The dot-product
The vector-matrix multiplication and matrix-vector multiplication definitions are equivalent.
Vector-matrix
Vector-matrix definition of matrix-matrix multiplication (A and B are matrix)
<MATH> \text{ row r of } (AB) = \underbrace{(\text{ row r of } A)}_{vector} * B </MATH>
<MATH> \underbrace{ \begin{bmatrix} \alpha_1 & \alpha_2 & \alpha_3 \\ \hline 2 & 1 & 0 \\ \hline 0 & 0 & 1 \end{bmatrix}}_{A} \begin{bmatrix}\begin{array}{rrr} & & \\ & \large{B} & \\ & & & \end{array}\end{bmatrix} = \begin{bmatrix} [\alpha_1, \alpha_2, \alpha_3] * B \\ \hline [2,1,0] * B \\ \hline [0,0,1] * B \end{bmatrix} </MATH>
<math>[\alpha_1, \alpha_2, \alpha_3]</math> * B can be (computed|interpreted) with the same result as:
Vector-matrix Linear Combination
A Linear combinations definition of vector-matrix multiplication (Ie the A vector is seen as the coefficient container that must be applied to the others vectors) <MATH>\alpha_1.[b_1] + \alpha_2.[b_2] + \alpha_3.[b_3]</MATH>
Implementation Pseudo-Code:
# Transform the matrix as Row Vectors
rowVectorDict = mat2rowdict(M)
# Multiply the row vector by the coefficient of the corresponding vector
rowVectorsWithCoef = [v[j]*rowVectorDict[j] for position j in rowVectorDict of B]
# Addition the vector
resultVector = sum(rowVectorsWithCoef)
Total Example:
def linear_combination_vector_matrix_multiplication(v, M):
assert(v.D == M.D[0])
rowVectorDict = mat2rowdict(M)
rowDictTimesVec = [(v.f[iDict] if iDict in v.f else 0)*rowVectorDict[iDict] for iDict in rowVectorDict]
return sum(rowDictTimesVec)
Vector-matrix Dot product
A Dot-product definition of vector-matrix multiplication is the multiplication of two vectors.
<MATH> \begin{array}{c} [1, 0, 0] * \begin{bmatrix} b_1 \\ \hline b_2 \\ \hline b_3 \end{bmatrix} = b_1 {\bf \text{ and } } [2, 1, 0] * \begin{bmatrix} b_1 \\ \hline b_2 \\ \hline b_3 \end{bmatrix} = 2b_1+b_2 {\bf \text{ and } } [0, 0, 0] * \begin{bmatrix} b_1 \\ \hline b_2 \\ \hline b_3 \end{bmatrix} = b_3 \\ {\bf \text{ therefore }} \begin{bmatrix} 1 & 0 & 0 \\ \hline 2 & 1 & 0 \\ \hline 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} b_1 \\ \hline b_2 \\ \hline b_3 \end{bmatrix} = \begin{bmatrix} b_1 \\ \hline 2 b_1 + b_2 \\ \hline b_3 \end{bmatrix} \end{array} </MATH>
<math> \begin{bmatrix} 1 & 0 & 0 \\ \hline 2 & 1 & 0 \\ \hline 0 & 0 & 1 \end{bmatrix} </math> is called an elementary row-addition matrix.
By matrix-vector definition of matrix-matrix multiplication, the result is a matrix with one column that you can interpret as a vector : a column vector
Implementation Dot Product Pseudo-code:
# Get the columns vector
# Dot product multiplication with the vector
Implementation:
def dot_product_vector_matrix_multiplication(v, M):
assert(v.D == M.D[0])
columnVectors = mat2coldict(M)
return Vec(M.D[1],{i:columnVectors[i]*v for i in M.D[1]})
Matrix-vector
Matrix-vector definition of matrix-matrix multiplication
<MATH> \mbox{ column s of } AB = A * \underbrace{(\text{ column s of } B)}_{vector} </MATH>
<MATH> A = \begin{bmatrix} \begin{array}{rr} 1 & 2 \\ \hline -1 & 1 \end{array} \end{bmatrix} {\bf \text{ and } } B= \begin{bmatrix} \begin{array}{r|r|r} 4 & 2 & 0 \\ 3 & 1 & -1 \end{array} \end{bmatrix} </MATH>
Matrix-vector Linear Combination
Pseudo-Code:
- Transform the A matrix as Column Vectors
<math> \begin{array}{rrr} columnVectorA_1 & = & \begin{bmatrix}1\\-1\end{bmatrix}\\ columnVectorA_2 & = & \begin{bmatrix}2\\1\end{bmatrix} \end{array} </math>
- Transform the B matrix as Column Vectors
<math> \begin{array}{rrr} columnVectorB_1 & = & \begin{bmatrix}4\\3\end{bmatrix}\\ columnVectorB_2 & = & \begin{bmatrix}2\\1\end{bmatrix} \\ columnVectorB_3 & = & \begin{bmatrix}0\\-1\end{bmatrix} \end{array} </math>
- Multiply each A column vector by the coefficient of the corresponding column vector of B to make a linear combination and addition the vector. Example for the first column vector of B (ie B1):
<math> \begin{array}{rrllll} columnVectorAB_1 & = & columnVectorB_1[0] * columnVectorA_1 & + & columnVectorB_1[1] * columnVectorA_2 \\ & = & 4 * columnVectorA_1 & + & 3 * columnVectorA_2 \\ & = & 4 * \begin{bmatrix}1\\-1\end{bmatrix} & + & 3 * \begin{bmatrix}2\\1\end{bmatrix} \\ & = & \begin{bmatrix}4*1\\4*-1\end{bmatrix} & + & \begin{bmatrix}3*2\\3*1\end{bmatrix} \\ & = & \begin{bmatrix}4\\-4\end{bmatrix} & + & \begin{bmatrix}6\\3\end{bmatrix} \\ & = & \begin{bmatrix}10\\-1\end{bmatrix} \end{array} </math>
- and restart the process for the next column vector of B to get the full matrix:
Total Example:
def linear_combination_matrix_vector_multiplication(M, v):
# assert the column domain is the domain of the vector
assert(M.D[1] == v.D)
colDict = mat2coldict(M)
colDictTimesVec = [(v.f[iDict] if iDict in v.f else 0)*colDict[iDict] for iDict in colDict]
return sum(colDictTimesVec)
Matrix-vector Dot Product
<MATH>\text{AB is the matrix with:}</MATH> <MATH>\text{column i of } AB = A * ( \text{column i of } B)</MATH>
<MATH> \begin{array}{lllllllllll} AB_{J1} & = & A * [4,3] & = & [[1,2]*[4,3], [-1,1]*[4,3]] & = & [1*4+2*3, -1*4+1*3] & = & [10,-1] \\ AB_{J2} & = & A * [2,1] & = & [[1,2]*[2,1], [-1,1]*[2,1]] & = & [1*2+2*1, -1*2+1*1] & = & [4,1] \\ AB_{J3} & = & A * [0,-1] & = & [[1,2]*[0,-1], [-1,1]*[0,-1]] & = & [1*0+2*-1, -1*0+1*-1] & = & [-2,-1] \end{array} </MATH> <MATH>AB = \begin{bmatrix} \begin{array}{r|r|r} 10 & 4 & -2 \\ -1 & 1 & -1 \end{array} \end{bmatrix} </MATH>
Implementation for one vector matrix:
def dot_product_mat_vec_mult(M, v):
assert (M.D[1] == v.D)
# Get the row vectors
rowVectors = mat2rowdict(M)
# Dot product multiplication with the vector
return Vec(M.D[0],{i:rowVectors[i]*v for i in M.D[0]})
Dot product
The Dot product definition of matrix-matrix multiplication is a combination of:
It's a inner_product.
Entry rc of AB is the dot-product of row r of A with column c of B.
<MATH> \begin{bmatrix} \begin{array}{ccc} 1 & 0 & 2 \\ \hline 3 & 1 & 0 \\ \hline 2 & 0 & 1 \end{array} \end{bmatrix} * \begin{bmatrix} \begin{array}{c|c} 2 & 1 \\ 5 & 0 \\ 1 & 3 \end{array} \end{bmatrix} = \begin{bmatrix} \begin{array}{c|c} [1,0,2]*[2,5,1] & [1,0,2]*[1,0,3] \\ [3,1,0]*[2,5,1] & [3,1,0]*[1,0,3] \\ [2,0,1]*[2,5,1] & [2,0,1]*[1,0,3] \end{array} \end{bmatrix} = \begin{bmatrix} \begin{array}{c|c} 4 & 7 \\ 11 & 3 \\ 5 & 5 \end{array} \end{bmatrix} </MATH>
Dot product Computation
where:
- C[1,1] = A[1,1]*B[1,1] + A[1,2]*B[2,1] + A[1,3]*B[3,1] + A[1,4]*B[4,1]
- C[1,1] = 1 * 1 + 3 * 4 + 4 * -3 + -2 * 0
- C[1,1] = 1
Formula: <MATH> [X.Y]_{i,j} = \sum_{r=1}^n X_{i,r} Y_{r,j} </MATH>
One-Vector Matrix (multiplication|product)
Two ways to multiply two vectors interpreted as matrices.
Inner product
Let u and v be two D-vectors interpreted as matrices.
Matrix-matrix product <math>u^T v</math> where:
- <math>u^T</math> is a row vector matrix
- <math>v</math> is a column vector matrix
Example: <MATH> [1 2 3] \begin{bmatrix} 3 \\ 2 \\ 1 \end{bmatrix} = [10] </MATH>
The first matrix has one row, the second matrix has one column, therefore the product has one entry.
Outer product
Another way to multiply vectors as matrices. The outer product of u and v
For any u and v, consider <math>{\bf uv}^T</math>
Example: <MATH> \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} [ v_1 v_2 v_3 v_4 ] = \begin{bmatrix} u_1v_1 & u_1{v_2} & u_1{v_3} & u_1{v_4} \\ u_2v_1 & u_2{v_2} & u_2{v_3} & u_2{v_4} \\ u_3v_1 & u_3{v_2} & u_3{v_3} & u_3{v_4} \\ \end{bmatrix} </MATH>
For each element s of the domain of u and each element t of the domain of v, the s, t element of <math>{\bf uv}^T</math> is <math>{\bf u}[s]{\bf v}[t]</math>
An Outer product is just a special case of general matrix multiplication that follows the same rules as normal matrix multiplication.
Legal
Definition
It is legal to multiply the matrix A times the matrix B if
- A is a R x S matrix, and
- B is a S x T matrix
The resulting matrix is a R * T matrix.
A*B, the columns in A must equal the rows in B. The size of the result will be A.rows by B.columns.
Example:
| A | B | Legal | AB | |||
|---|---|---|---|---|---|---|
| Rows | Columns | Rows | Columns | Rows | Columns | |
| 2 | 3 | 2 | 3 | Not Legal | ||
| 1 | 3 | 3 | 2 | Legal | 1 | 2 |
| 1 | 3 | 3 | 1 | Legal | 1 | 1 |
| 3 | 1 | 1 | 3 | Legal | 3 | 3 |
Transpose
- For <math>AB</math> to be legal, <math>A</math> ’s column labels = <math>B</math> ’s row labels.
- For <math>A^T.B^T</math> to be legal, <math>A</math> ’s row labels = <math>B</math> ’s column labels.
| Legal / Illegal | Tranpose formule |
|---|---|
| Legal | <math>(AB)^T = B^T A^T</math> |
| Illegal It doesn’t even make sense (it's not legal) | <math>(AB)^T = A^T.B^T</math> |
<MATH> \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} * \begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix} \text{ is legal but } \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix} * \begin{bmatrix} 6 & 8 \\ 7 & 9 \end{bmatrix} \text{ is not } </MATH>
Property
Commutativity
AB is not commutative. AB is different from BA.
One product might be legal while the other is illegal
Inverse
- Let A, B, M be matrix,
- Let <math>B = MA</math> ,
- Let M be Linear Algebra - Matrix and has then an inverse <math>M^{-1}</math> ,
- Then <math>M^{-1}B = A</math>
Others
SQL
In sparse matrix format (i, j, value)
SELECT MatrixA.row_num,
MatrixB.col_num,
SUM(MatrixA.value * MatrixB.value) value
FROM a MatrixA,
b MatrixB
WHERE MatrixA.col_num = MatrixB.row_num
GROUP BY MatrixA.row_num,
MatrixB.col_num