Statistics - Bias-variance trade-off (between overfitting and underfitting)
About
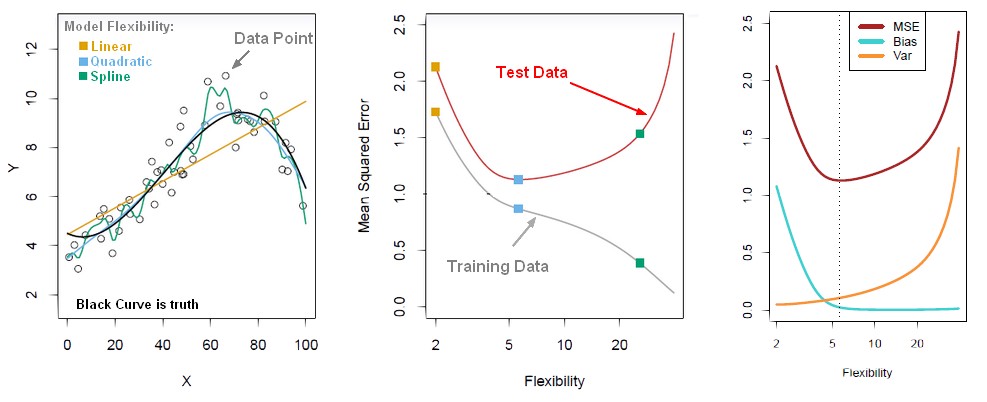
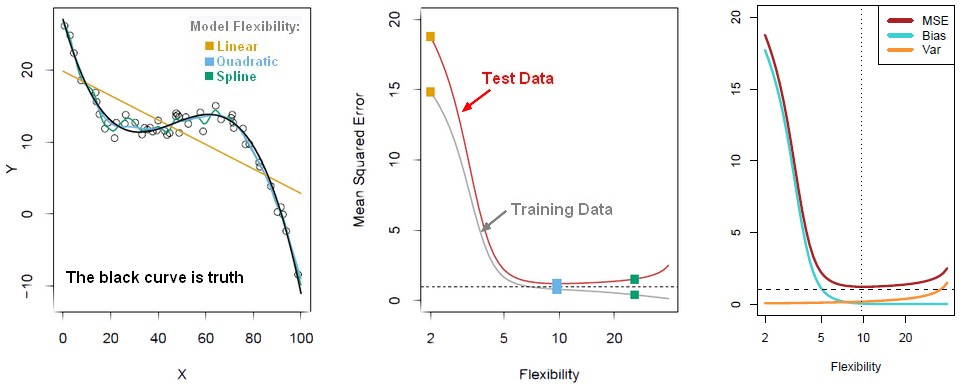
The bias-variance trade-off is the point where we are adding just noise by adding model complexity (flexibility). The training error goes down as it has to, but the test error is starting to go up. The model after the bias trade-off begins to overfit.
When the nature_of_the_problem is changing the trade-off is changing.
Articles Related
Formula
The ingredients of prediction error are actually:
- bias: the bias is how far off on the average the model is from the truth.
- and variance. The variance is how much that the estimate varies around its average.
Bias and variance together gives us prediction error.
This difference can be expressed in term of variance and bias:
<math>e^2 = var(model) + var(chance) + bias</math>
where:
- <math>var(model)</math> is the variance due to the training data set selected. (Reducible)
- <math>var(chance)</math> is the variance due to chance (Not reducible)
- bias is the average of all <math>\hat{Y}</math> over all training data set minus the true Y (Reducible)
As the flexibility (order in complexity) of f increases, its variance increases, and its bias decreases. So choosing the flexibility based on average test error amounts to a bias-variance trade-o ff.
Illustration
where:
- Model complexity are important techniques to fit better a data set (ie to reduce the prediction error).
We want to find the model complexity that gives the smallest test error.
When the nature_of_the_problem is changing the trade-off is changing.
Nature of the problem
When the nature of the problem is changing the trade-off is changing.
- the truth is wiggly and the noise is high, so the quadratic do the best
- the truth is smoother, so the linear model do really well
- the truth is wiggly and the noise is low, so the more flexible do the best
Model Complexity is better/worse
Model Complexity = Flexibility
- The sample size is extremely large, and the number of predictors is small: Flexible is better. A flexible model will allow us to take full advantage of our large sample size.
- The number of predictors is extremely large, and the sample size is small: Flexible is worse. The flexible model will cause overfitting due to our small sample size.
- The relationship between the predictors and response is highly non-linear. A flexible model will be necessary to find the nonlinear effect.
- The variance of the error terms, i.e. sigma^2 = var(Epsilon) , is extremely high: Flexible is worse. A flexible model will cause us to fit too much of the noise in the problem.