About
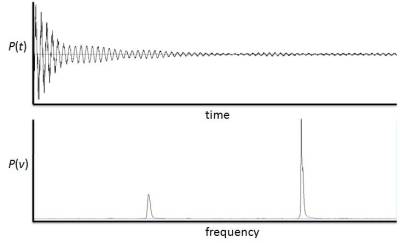
A fast Fourier transform (FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse.
Fourier analysis converts:
and vice versa
An FFT rapidly computes such transformations by factorizing the discrete Fourier transform (DFT) matrix into a product of sparse (mostly zero) factors.
In 1994 Gilbert Strang described the fast Fourier transform as “the most important numerical algorithm of our lifetime” and it was included in Top 10 Algorithms of 20th Century by the IEEE journal Computing in Science & Engineering.