Mathematics - Complex Exponential (Euler's formula)
About
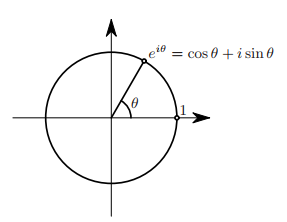
Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions (the sinusoidal functions) as weighted sums of the exponential function.
<MATH> e^{i\theta} = \cos \theta + i\sin \theta \\ e^{i\pi} = -1 </MATH>
where:
- cos x + i * sin x is an complex number where i is the imaginary unit
- the argument x is given in radians.