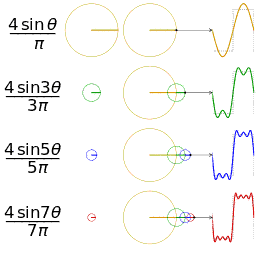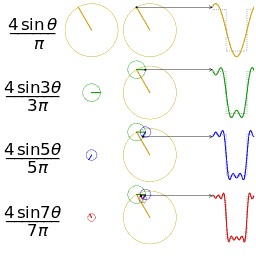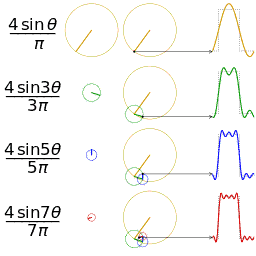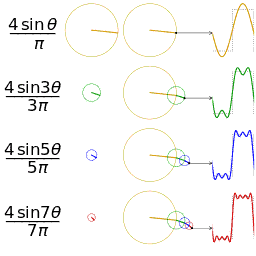About
The Fourier Series breaks down a periodic function into the sum of sinusoidal functions.
A Fourier series is a way to represent a wave-like function (like a square wave) as the sum of simple sine waves.
The Fourier Series decomposes any periodic function or periodic signal into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or, equivalently, complex exponentials).
The Fourier Series is the Fourier Transform for periodic functions.
- period P
- frequency <math>\frac{1}{P}</math>
- An infinite sum = series
Articles Related
Definition
A Fourier Series, with period T, is an infinite sum of sinusoidal functions (cosine and sine), each with a frequency that is an integer multiple of <math>\frac{1}{T}</math> (the inverse of the fundamental period).
Documentation / Reference
- Fourier Series by Jim.belk - Own work. Licensed under Public Domain via Wikimedia Commons