Geometry - Object

Viz - Graphic Object in Geometry

An object can be:

• a pre-defined shape
• or an arbitrary one defined with the help of a path.

Notions such as:

• The length of a vector
• The angle between two vectors.

are introduced with the inner product of two vectors

A geometric object (point, line, plane, …) which contains the origin can be representing by a subset of in two different ways :

• Span of some vectors
• Solution set of some system of linear equations with zero right-hand sides

Representation	Line	Plan
Picture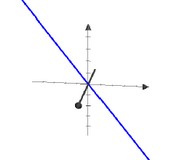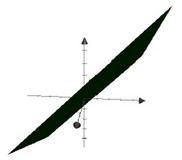
Span of some vectors ( subset of )	The Span of one “3-vectors” is a line through the origin in three dimensions Span {[1, 2, -2]}	The Span of two “3-vectors” is a plane through the origin in three dimensions Span {[4,-1,1], [0, 1, 1]} This plane contains this two lines: - Span {[4,-1,1]} - Span {[0,1,1]}
Solution set of system of linear equations with zero right-hand sides ( subset of )	{[x, y, z] : [1,2,-2] . [x, y, z] = 0}	{[x, y, z] : [4,-1, 1].[x, y, z] = 0, [0, 1, 1].[x, y, z] = 0}

• Point: Zero-dimensional: Span of the empty set: The origin

A geometric object (point, line, plane, …) can be expressed as the solution set of a system of linear equations.

<math>\{x : \alpha_1 . x = \beta_1 , ... \alpha_n = \beta_n\}</math>