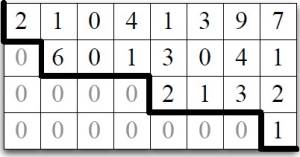
Linear System - Echelon Matrix
Table of Contents
About
The Echelon form is a generalization of triangular matrices.
An <math>m * n</math> matrix A is in echelon form if it satisfies the following condition:
- for any row, if that row’s first nonzero entry is in position k
- then every previous row’s first nonzero entry is in some position less than k.
