Definition
For each input element in a set <math>A</math> , a function assigns a single output element from another set <math>B</math> .
!!!!!! Same as Set Theory - Function (Mathematical) !!!!!!
Articles Related
Syntax
<math>f(A) = B</math>
or in Mathese:
<math>f : A \rightarrow B</math>
Example
- The function that doubles its input:
f({1, 2, 3,...}) = {(1,2),(2,4),(3,6),(4,8),....}
- The function that multiplies the numbers forming its input:
f({1, 2, 3,...}x{1, 2, 3,...}) = {((1,1),2),((1,2),4),...,((2,2),4),(2,3),6), ....}
- Caesar’s Cryptosystem
Each letter is mapped to one three places ahead, wrapping around, so MATRIX would map to PDWULA. The function mapping letter to letter can be written as:
{('A','D'),('B','E'),('C','F'),('D','G'),...,('W','Z'),('X','A'),('Y','B'),('Z','C')}
Both the domain and the co-domain are {A,B, …,Z}
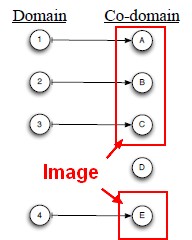
Image
for a function <math>f : V \mapsto W</math> , the image of f is the set of all images of elements of the domain: <MATH> {f (v) : v \in V} </MATH>
The image of a function is the set of all images of inputs. Mathese:
lm f
The output of a given input is called the image of that input. The image of A under the function f is denoted f(A).
There might be elements of the co-domain that are not images of any elements of the domain.
| Example | |
|---|---|
| A function f : {1, 2, 3, 4} −> {'A','B','C','D','E'} The image of f is lm f = {'A','B','C','E'} 'D' is in the co-domain but not in the image |  |
Set
Set of functions: For sets F and D, <math>F^D</math> denotes all functions from D to F.
For finite sets, the cardinality <math>|F^D| = |F|^{|D|}</math>
Function
Identity
Composition
Inverse
Functions f and g are functional inverses if
f circ gand
g circ fare defined and are identity functions.
Invertible
A function that has an inverse is invertible.
Invertible functions are:
Function Invertibility Theorem: A function f is invertible if and only if it is one-to-one and onto.
Linear-Function Invertibility Theorem: A function <math>f: V \mapsto W</math> is invertible iff
- <math>\text{dim Ker f = 0 and dim lm f = dim W }</math>
- <math>\text{dim Ker f = 0 and dim V = dim W }</math> (For f to be invertible, need dim V = dim W)
Extracting an invertible function:
Let <math>A = \begin{bmatrix} \begin{array}{r|r|r} 1 & 2 & 1 \\ 2 & 1 & 1 \\ 1 & 2 & 1 \\ \end{array} \end{bmatrix} </math> and define <math>f : \mathbb{R}^3 \mapsto \mathbb{R}^3</math> by <math>f (x) = Ax</math>
Define <math>W^* = lm f = Col A = Span \{[1, 2, 1], [2, 1, 2], [1, 1, 1]\}</math>
One basis for <math>W^*</math> is:
- <math>w_1 = [0, 1, 0]</math> ,
- <math>w_2 = [1, 0, 1]</math>
Pre-images for <math>w_1</math> and <math>w_2</math> :
- <math>v_1 = [\frac{1}{2},−\frac{1}{2},\frac{1}{2}]</math>
- and <math>v_2 = [−\frac{1}{2},\frac{1}{2},\frac{1}{2}]</math>
for then <math>A.v_1 = w_1</math> and <math>A.v_2 = w_2</math>
Let <math>V^* = Span \{v_1, v_2\}</math> Then <math>f : V^* \mapsto lm f </math> is onto and one-to-one and therefore invertible.
Linear
Relationship
One-to-one
<math>f : V \rightarrow W</math> is one-to-one if f (x) = f (y) implies x = y
One-to-One Lemma: A linear function is one-to-one if and only if its kernel is a trivial vector space. Equivalent: if its kernel has dimension zero.
f is one-to-one iff <math>\href{dimension}{dim} \text{ } \href{#kernel}{Ker} \text{ } f = 0</math>
Onto
<math>f : V \rightarrow W</math> is onto if for every <math>z \in F</math> there exists an a such that <math>f(a) = z</math>
f is onto if its image equals its co-domain
For any linear function <math>f : V \mapsto W</math> , f is onto if <math>\href{dimension}{dim} \text{ } \href{#image}{lm} f = \href{dimension}{dim} \text{ } W</math>