About
Functions + Class - Composition (Composite | Component)
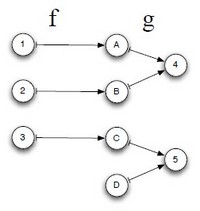
- <math>f : A \rightarrow B</math>
- and <math>g : B \rightarrow C</math>
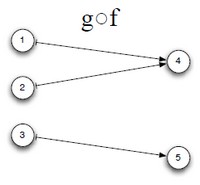
the functional composition of f and g is the function:
- <math>(g \circ f) : A rightarrow C</math>
defined by:
- <math>(g \circ f)(x) = g(f (x))</math>
Articles Related
Example
| Example | <math>g \circ f</math> |
|---|---|
| <math>f : \lbrace {1, 2, 3} \rbrace \rightarrow \lbrace { A, B, C, D } \rbrace</math>
<math>g : \lbrace{A, B, C, D}\rbrace \rightarrow \lbrace{4, 5}\rbrace</math> |  |
| <math>g(y) = y%%^%%2</math>
<math>f(x) = x + 1 </math> <math>(g \circ f)(x) = (x + 1)%%^%%2</math> |  |
| <math>f: \lbrace {A, B, C, ..., Z} \rbrace \rightarrow \lbrace {0, 1, 2, ..., 25}\rbrace</math>
<math>g(x) = (x+3) mod 26</math> <math>h: \lbrace{A, B, C, ..., Z}\rbrace \rightarrow \lbrace{0, 1, 2, ..., 25}\rbrace</math> <math>h \circ (g \circ f)</math> is the Caesar cypher |   |
Associativity
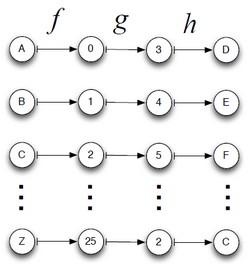
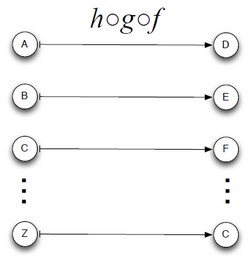
Associativity of function composition: <math>h \circ (g \circ f) = (h \circ g) \circ f</math>
<math>(h \circ (g \circ f))(x)</math> =
- <math>h(g \circ f)(x)</math>
- <math>h(g(f(x)))</math>
- <math>(h \circ g)(f(x))</math>
- <math>((h \circ g) \circ f)(x)</math>