About
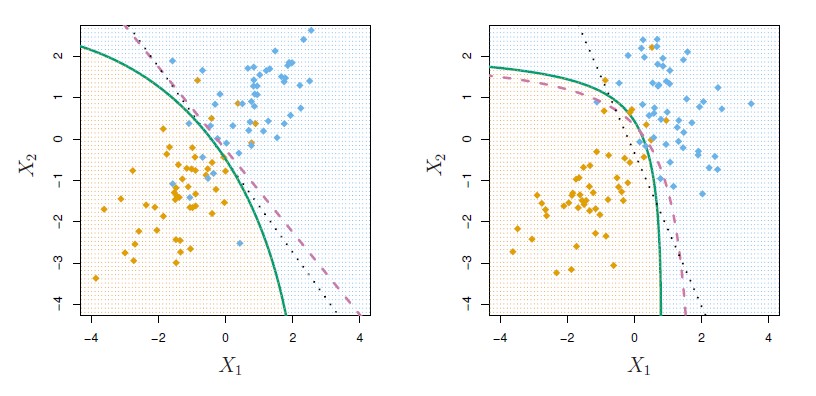
When the variances of all X are different in each class, the magic of cancellation doesn't occur because when the variances are different in each class, the quadratic terms don't cancel.
And therefore , the discriminant functions are going to be quadratic functions of X.
Quadratic discriminant analysis uses a different covariance matrix for each class.
Quadratic discriminant analysis is attractive if the number of variables is small.
Articles Related
Discriminant Function
<MATH> \delta_k(x) = - \frac{1}{2} (x - \mu_k)^T \sum^{-1}_k ( x - \mu_k) + log(\pi_k) </MATH>
As there's no cancellation of variances, the discriminant functions now have this distance term that involves <math>\sum_k</math> , which is for the kth class.
There's :
- a term to do with the prior probability,
- a determinant term that comes from the covariance matrix.
It gives a curved discriminant boundary.