About
A normal distribution is one of underlying assumptions of a lot of statistical procedures.
In nature, every outcome that depends on the sum of many independent events will approximate the Gaussian distribution after some time, if respected the assumptions of the Central limit theorem.
Data from physical processes typically produce a normal distribution curve.
Because of the Central limit theorem, the normal distribution plays a fundamental role in probability theory and statistics.
The normal distribution is commonly denoted as <math>N(0,1)</math> .
Articles Related
Properties
The properties of a normal distribution are well-known:
- the data distribution is well known:
- The mean is at the middle (50% of the data are above and 50% of the data are below)
- 68% of the data fall between -1 and 1 standard deviation
- 95% of the data fall between -2 and 2 standard deviation
- 99.7% of the data fall between -3 and 3 standard deviation
- the measures of center (Mean, Median and Mode) will be just about the same.
- the distribution is symmetric
See density for the function
Explication
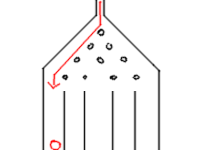
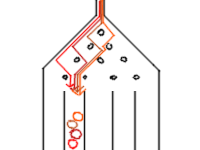
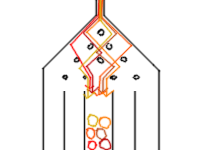
Considering the classic bean machine (Galtonboard, Galtonbrett Simulation, quincunx or Galton).
The Galtonboard is a device invented by Sir Francis Galton to demonstrate the central limit theorem, in particular that the normal distribution is a good approximate to the binomial distribution.
 | There's only one way for a ball to reach the first column |
 | There are four ways to reach the second column |
 | There are six ways to reach the third column |
 | Because the machine is symetrical, after some time it will look like a gaussian distribution |
Function
Density
The Gaussian function (density) has the form:
<MATH> f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{\displaystyle -\frac{1}{2} \left (\frac{x-\mu}{\sigma} \right )^2} </MATH>
where:
- <math>\mu</math> is the mean
- <math>\sigma</math> is the standard deviation
As notated on the figure, the probabilities of intervals of values correspond to the area under the curve.
Cumulative
The cumulative distribution function (CDF) is noted <math>\Phi(z)</math> .
where:
- <math>\mu</math> is the mean
- <math>\sigma</math> is the standard deviation
Approximation
Trigonometry - (Cosine|Cosinus) <MATH> f(x) = \frac{1+cos(x)}{2\pi} </MATH> This approximation can be integrated in closed form