About
The probability of an event is the subjective chance that it will happen.
The laws of probability are heavily build with the random notion.
A probability is a non-negative number between 0 and 100%.
If you add all the possible event on the x axis, you get a probability distribution.
To verify the the result, you can simulate the event through the creation of a script.
Articles Related
The probability of you being born was about 1 in 400 trillion.
Event
One
<MATH> \text{Probability of event A} = \frac{\text{Number of possible outcomes fitting our criteria}}{\text{Total number of possible outcomes}} = P(A) </MATH>
<MATH> \text{Odds of event} = \frac{\text{Number of successes}}{\text{Number of non-successes}} </MATH>
If the probability of an event is 3/5, the odds are 3/2.
Independent
If the events are independent, we can multiply each probability. Two events are independent when the outcome of the first event does not influence the outcome of the second event.
<MATH> P(A \text{ and } B) = P(A) . P(B) </MATH>
Dependent
Two events are dependent when the outcome of the first event influences the outcome of the second event. see Statistics - Bayes’ Theorem (Probability)
<MATH> P(A \text{ and } B) = P(A) . P(B \text{ after } A) </MATH>
Example: Probability to choose 2 red cards in a deck of 52 cards. <MATH> P(\text{Red card}) = \frac{26}{52} </MATH>
<MATH> P(\text{2 Red cards}) = \frac{26}{52} . \frac{25}{51} </MATH>
Exclusive
Exclusive events cannot happen at the same time.
<MATH> P(A \text{ or } B) = P(A) + P(B) </MATH>
Example:
- wheel of fortune, only one field can be chosen. The chance to go the field 1 or 2.
- the chance that two persons will stay at the same hotel in a set of 3 hotels (A, B, C)
<MATH> P(A \text{ or } B \text{ or } C) = P(A) + P(B) + P(C) = (\frac{1}{3}.\frac{1}{3}) + (\frac{1}{3}.\frac{1}{3}) + (\frac{1}{3}.\frac{1}{3}) = \frac{3}{9} = = \frac{1}{3} </MATH>
Inclusive
Inclusive events can happen at the same time.
<MATH> P(A \text{ or } B) = P(A) + P(B) - P(A \text{ and } B) </MATH>
Example: What is the probability of drawing a black card or a ten in a deck of cards? This probability is inclusive because you can have in one event the two possibles outcomes.
- Event A: drawing a black card: 26 outcomes
- Event B: drawing a ten card: 4 outcomes
- Event A and B: drawing a ten black card: 2 outcomes
- Total of possible outcomes: 52 cards
<MATH> P(A \text{ or } B) = \frac{26}{52} + \frac{4}{52} - \frac{2}{52} </MATH>
Category
Frequency
For the frequentist a hypothesis is a proposition (which must be either true or false), so that the frequentist probability of a hypothesis is either one or zero.
Evidential
In Bayesian statistics, a probability can be assigned to a hypothesis that can differ from 0 or 1 if the true value is uncertain.
Propensity
A coin is tossed repeatedly many times, in such a way that its probability of landing heads is the same on each toss, and the outcomes are probabilistically independent, then the relative frequency of heads will (with high probability) be close to the probability of heads on each single toss. This law suggests that stable long-run frequencies are a manifestation of invariant single-case probabilities.
Frequentists are unable to take this approach, since relative frequencies do not exist for single tosses of a coin, but only for large ensembles or collectives. Hence, these single-case probabilities are known as propensities or chances.
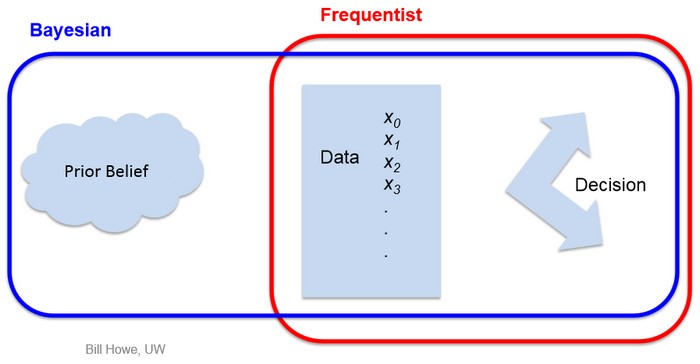
Bayesian and Frequentist Concepts
Differences between Bayesian and Frequentist Concepts
| Frequentist | Bayesian |
|---|---|
| Data are a repeatable random sample (there is a frequency) | Data are observed from the realized sample |
| Underlying parameters remain constant during this repeatable process | Parameters are unknown and described probabilistically |
| Parameters are fixed | Data are fixed |
I declare the Bayesian vs. Frequentist debate over for data scientists | Simply Statistics